

This lack of a zero may seem as if it would have been a big problem. These same symbols could also be 3,660, if you imagine the space after the number. It would have been hard to tell if you had a space or not. Both have a 1, then another 1, but 3601 would have a space in between. Because of this lack of a zero, the symbols for 3,601 would have looked the same as the symbols for 61. There was one problem with the Babylonian number system – it did not have a symbol for zero. The Babylonians Did Not Have a Symbol for Zero Question 2: Convert the number 7812 into Babylonian. Tip: this is one number, in three separate place values, with | being the best the computer can do to show the Babylonian symbol for 1! Question 1: Convert the Babylonian number | ||| || into Hindu Arabic (our system).
#Babylonian numerals conversion plus#
If we place 1 in the 3,600 place, we have 3,600 – 3,670 = 70 left, which is one 60, plus 10 left over: The next place value is 3600 because the place values were powers of 60, and 60 2 = 3600. Now we have a number large enough to need the next place value – the 3,600’s place. We start by dividing: 683 ÷ 60 = 11.38333…Since the system was base 60, the Babylonians could have up to the number 59 in any given place value, so putting 11 in one place value was just fine! Since 11 × 60 = 660, there was 683 – 660 = 23 left for the ones place.Įxample 4 Convert the number 3,670 to Babylonian. Answers to both questions are here.Įxample 3 Convert the number 683 to Babylonian.

Question 2: Convert the number 187 into Babylonian. Question 1: Convert the number 67 into Babylonian. We know there are three left for the ones place because 2 × 60 = 120, and 123 – 120 = 3. To make the number 123 in Babylonian, since 123 ÷ 60 = 2.05, we know there are two 60’s.
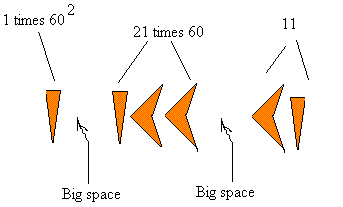
Since the system was base 60, this one was actually worth 60, similar to the way in which in the Hindu Arabic number 102, the 1 is actually worth 100.Įxample 2 Convert the number 123 to Babylonian. The space between the sets of symbols indicates that the first symbol for one is in a separate place value from the next two symbols. For example, 36 was made with 3 tens and 6 ones:īut the Babylonian system was actually a base 60, place value system, with place values of 60 0 = 1, 60 1 = 60, 60 2 = 3600, etc.Įxample 1 Convert the number below to our system (Hindu Arabic). At first glance, the system may seem additive, because they created the numbers from 1 to 59 by combining the ones and tens symbols.


 0 kommentar(er)
0 kommentar(er)
